Højdevækstfunktioner for bøg, eg, rødgran, sitkagran, ædelgran og douglasgran
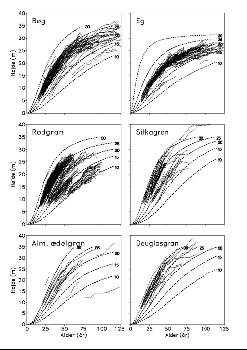
Figur 1. Observerede højdevækstforløb for bøg, eg, rødgran, sitkagran, ædelgran og douglasgran samt de skønnede vækstforløb for forskellige højdeboniteter. Højdeboniteten er angivet som den forventede overhøjde ved alder 50 år.
Dette Videnblad beskriver nye højdevækstfunktioner for bøg, eg, rødgran, sitkagran, alm. ædelgran og douglasgran. Funktionerne afløser de gamle indtegnede bonitetskurver og tilvækstoversigter, som ikke længere er tidssvarende.
De nye funktioner er baseret på en matematisk tilpasning af data fra Skov & Landskabs langsigtede forsøg. Højdevækstfunktionerne er dokumenteret i detaljer i en videnskabelig artikel af Nord-Larsen et al. (2009).
Taksation af langsigtede forsøg
Data stammer fra 279 langsigtede produktions-, afstands- og tyndingsforsøg med i alt 815 parceller. Materialet er indsamlet i perioden 1872 til 2008, hvor de enkelte bevoksninger er observeret over en periode på mellem 10 og 126 år. Det samlede antal taksationer er 1644 for bøg, 1424 for eg, 2554 for rødgran, 616 for sitkagran, 170 for ædelgran og 300 for douglasgran.
Ved hver taksation blev diameteren af samtlige træer målt ved korsvis klupning i brysthøjde. Højden blev målt på gennemsnitligt 23,4 stående og 8,6 fældede træer per parcel. På baggrund af sammenhørende målinger af diameter og højde blev der konstrueret en diameter-højde regression, og ved hjælp af denne blev højden af de øvrige træer bestemt. Slutteligt blev overhøjden bestemt som gennemsnitshøjden af de 100 tykkeste træer per hektar.
Den matematiske model
Den matematiske model blev tilpasset de observerede højdevækstforløb fra prøve-fladerne ved en statistisk metode, hvor bevoksningsalderen (fra frø) optræder som uafhængig variabel og overhøjden som afhængig variabel. Metoden er objektiv og resulterer i den bedst mulige kurve gennem de observerede data.
Den valgte model er oprindeligt formuleret af Cieszewski (2003) og estimerer overhøjden (Ht) ved en given alder (t) ud fra en given højde (H0) ved alderen t0. Ved estimation af modellen indgår H0 som en parameter, der er specifik for den enkelte bevoksning og derfor udtrykker bevoksningens forventede højde ved indeksalderen (eks. t0=50 år).
Modellen kan udtrykkes matematisk som:
hvor:
og β1 – β3 er modellens parametre.
Modellen giver den estimerede kurve et S-formet forløb, hvor højdevæksten i den helt unge bevoksning er langsom, men tiltagende. Tilvæksten kulminerer i bevoksningens ungdom og er herefter aftagende i resten af bevoksningens levetid. I helt gamle bevoksninger bliver tilvæksten næsten lig 0.
Anvendelse af modellen
Sammenlignet med observerede vækstforløb for de forskellige træarter giver den matematiske model en god tilpasning til de faktiske forløb (figur 1). Dette kan også ses ud fra, at forklaringsgraden (R2) er høj (> 0,98) for alle seks træarter (tabel 1).
| Art | β1 | β2 | β3 | R2 |
| Bøg | 1,7644 | 3.472,7999 | 36,8037 | 0,991 |
| Eg | 1,6277 | 1,0000 | 31,9667 | 0,990 |
| Rødgran | 2,0323 | 6.448,8721 | 32,5165 | 0,984 |
| Sitkagran | 2,1538 | -2.870,2666 | 38,8603 | 0,984 |
| Alm. ædelgran | 2,1708 | 140.568,7517 | 20,4927 | 0,989 |
| Douglasgran | 1,8000 | 1,0000 | 44,4553 | 0,989 |
Tabel 1. Træartsvise parameter-estimater (β1 – β3) for højdevækstfunktionerne, samt modellens forklaringsgrad (R2)
De nye højdetilvækstfunktioner kan enkelt anvendes til at bestemme højdeboniteten ud fra en observation af bevoksningsalder og -højde ved at indsætte de artsspecifikke parameterestimater, bevoksningshøjden (H0), bevoksningsalderen (t0) og den ønskede indeksalder (f.eks. 50 år) i ligningen ovenfor. Ligeledes kan den forventede bevoksningshøjde (H) ved enhver anden bevoksningsalder (t) bestemmes ud fra højdeboniteten, dvs. den opnåede bevoksningshøjde (H0) ved indeksalderen (t0).
Eksempel
Lad os eksempelvis betragte en 31-årig rødgran bevoksning med en overhøjde på 19,2 m. Vi ønsker at bestemme overhøjden ved en indeksalder på 50 år. Vi kan beregne den forventede højde som:
Højde ved 50 år er altså 30,3 meter, hvilket cirka svarer til en bonitet lidt over 1 efter Møller (1933). Metoden kan også bruges til at bestemme den forventede højde ved en given alder, når boniteten er kendt, idet man så blot indsætter indeksalderen og boniteten på udtrykkets højre side.
Litteratur
Cieszewski, C.J. 2003: Developing a well-behaved dynamic site equation using a modified Hosfeld IV equation y3=(axm)/(c+xm-1), a simplified mixed-model and scant subalpine fir data. Forest Science 49: 539-554.
Møller, C.M. 1933: Boniteringstabeller og bonitetsvise Tilvækstoversigter for Bøg, Eg og Rødgran i Danmark. DST 18:537-623.
Nord-Larsen, T., Meilby, H., Skovsgaard, J.P. 2009: Site-specific height growth models for six common tree species in Denmark. Scandinavian Journal of Forest Research 24: 194-204.
Videnblad nr.: 09.02-08
Forfattere: Thomas Nord-Larsen, Henrik Meilby og Jens Peter Skovsgaard



